English
عربى
中文
Deutsch
Español
Français
हिन्दी
Hrvatski
Italiano
日本語
Português
Română
Русский
Svenska
Türkçe
Tiếng ViệtUntitled Courseプラトンの固体
このコースの最初に、すべての辺と角度が同じである
_通常の多面体では、_すべての 多面体の__面__は、その表面を構成するポリゴンです。 多面体の「コーナー」はその__頂点__と呼ばれます。 プラート（紀元前425年〜347年頃）は古代ギリシャの哲学者であり、彼の教師ソクラテスと彼の学生アリストテレスとともに、西洋の哲学と科学の根幹を築きました。 プラトンは、アテネアカデミーを設立しました。これは、西洋世界で最初の高等教育機関です。哲学と神学、科学と数学、政治と正義に関する彼の多くの著作は、彼を史上最も影響力のある思想家の一人にしています。 __プラトンソリッド__は、すべての面が同じ数のエッジを持つ正多角形であり、同じ数の面がすべての頂点で交わる多面体です。プラトンの立体は5つしかありません。4面体、立方体、8面体、12面体、20面体です。
それでは、プラトンの固体はどのように見え、それらの数はいくつですか？ 3次元形状を作成するには、すべての頂点で交わる面が少なくとも
3つの __正三角形__は、3つの辺すべてが同じ長さの三角形です。
4つの正三角形がすべての頂点で交わると、異なるプラトニックソリッドが得られます。 __八面体__と呼ばれ、
また、すべての頂点に7つ以上の三角形が存在しても、新しい多面体は生成されません。頂点の周囲に十分なスペースがないため、その数の三角形に適合しません。
これは、三角形で構成される
次に、通常の五角形を試してみましょう。
以前と同様に、4つ以上の五角形
次に試す正多角形は六角形です。
3つの六角形がすべての頂点で交わると、すぐに
同じことが、6辺を超えるすべての通常のポリゴンにも起こります。それらはテッセレーションせず、3次元のポリゴンも得られません。
つまり、プラトニックソリッドは
四面体
キューブ
八面体
正十二面体
正二十面体
面と頂点の数が すべて
すべての面を頂点で、すべての頂点を面で「置き換える」ことにより、多面体をその双対に変えることができます。これらのアニメーションは、次の方法を示しています。
四面体はそれ自体と二重です。同じ数の面と頂点があるので、それらを交換しても何も変わりません。
プラート（紀元前425年〜347年頃）は古代ギリシャの哲学者であり、彼の教師ソクラテスと彼の学生アリストテレスとともに、西洋の哲学と科学の根幹を築きました。 プラトンは、アテネアカデミーを設立しました。これは、西洋世界で最初の高等教育機関です。哲学と神学、科学と数学、政治と正義に関する彼の多くの著作は、彼を史上最も影響力のある思想家の一人にしています。
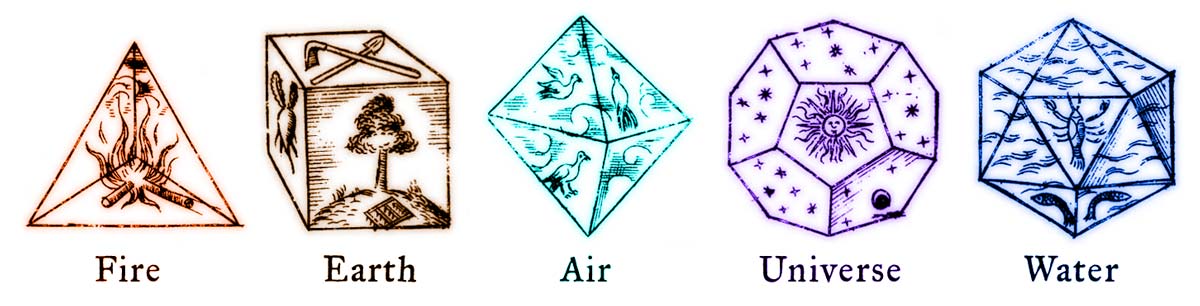
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)
アルキメデスの固体
プラトンの立体は特に重要な多面体ですが、他にも無数にあります。
たとえば、 __アルキメデスの立体__は、さまざまな種類の正多角形で構成された多面体で、どの方向から見ても同じです。 13種類のアルキメデスの立体があります。 アルキメデス（紀元前287年〜212年前）は、古代ギリシャの科学者でありエンジニアであり、史上最高の数学者の1人でした。彼は微積分学の多くの概念を発見し、幾何学、分析、力学に従事しました。 入浴中に、アルキメデスは不規則な物体の体積を、水没時に変位した水の量を使用して決定する方法を発見しました。彼はこの発見に非常に興奮していたので、服を脱いでいて、「エウレカ！」（_「私はそれを見つけた！」_のギリシャ語）を叫んで、通りを走り去りました。 エンジニアとして、彼は故郷のシチリア島シラキュースの包囲中に独創的な防御機械を構築しました。 2年後、ローマ人はついに侵入し、アルキメデスは殺された。彼の最後の言葉は、_「私のサークルの邪魔をしないでください」_でした–彼はその時に勉強していました。
切頂四面体 8面、12頂点、18エッジ
立方八面体 14面、12頂点、24エッジ
切り詰められたキューブ 14面、24頂点、36エッジ
切頭八面体 14面、24頂点、36エッジ
菱形立方八面体 26面、24頂点、48エッジ
切り捨てられた立方八面体 26面、48頂点、72エッジ
スナブキューブ 38面、24頂点、60エッジ
正十二面体 32面、30頂点、60エッジ
切頭十二面体 32面、60頂点、90エッジ
切頂二十面体 32面、60頂点、90エッジ
菱形二十面体 62面、60頂点、120エッジ
切頂正二十面体 62面、120頂点、180エッジ
十二面体 92面、60頂点、150エッジ
用途
プラトンは、すべての要素がプラトンの固体で構成されていると信じていたのは間違いでした。しかし、通常の多面体には、自然のどこかに現れるような多くの特別な特性があり、これらの特性を科学や工学にコピーすることができます。
Radiolaria skeleton
Icosahedral virus
多くの__ウイルス__ 、 細菌 、その他の小さな__生物__は、 __20面体__はプラトンの立体であり、すべて正三角形である20個の面で構成されています。 12個の頂点と30個のエッジがあります。
Buckyball molecule
Montreal Biosphere
多くの__分子__は通常の多面体のような形をしています。最も有名な例は __Truncated Icosahedron__は、12個の正五角形と20個の正六角形で構成される_アルキメデスの立体_です。
それは科学者が星間塵を研究したときに1985年に発見されました。彼らは、似たような建物の建設で有名な建築家 リチャードバックミンスター「バッキー」フラー（1895 – 1983）は、アメリカの建築家、デザイナー、発明家でした。彼は_geodesic dome_を構築することで有名です–大きな球状の構造物。同様に見える炭素分子である_フラーレン_は、後に彼にちなんで名付けられました。
Fluorite octahedron
Pyrite cube
ほとんどの__結晶__は、 __四面体__はプラトンの立体であり、正三角形である4つの面で構成されています。 4つの頂点と6つのエッジがあります。 立方体（__六面体__と呼ばれることもあります）は、すべての面が正方形である通常の多面体です。 5つの_プラトンソリッド_の1つであり、6つの面、8つの頂点、12のエッジがあります。 __八面体__はプラトンの立体であり、正三角形である8つの面で構成されています。 6つの頂点と12のエッジがあります。
Octagonal space frames
Louvre museum in Paris
四面体と八面体は非常に剛性が高く安定しているため、 __建設__に非常に役立ちます。 _スペースフレーム_は、大きな屋根や重い橋を支えることができる多角形構造です。
Football
Polygonal role-playing dice
プラトンの固体はまた、 __サイコロ__を作成するために使用されます。対称性があるため、すべての面で上向きに着地する __確率__は、特定のイベントが発生する可能性を示す0〜1の数値です。イベントの確率_A_は
__Truncated Icosahedron__は、12個の正五角形と20個の正六角形で構成される_アルキメデスの立体_です。