Untitled Courseテッセレーション

ポリゴンは自然界のいたるところに現れます。大きな領域を並べて表示する場合は、ギャップやオーバーラップなしでポリゴンを組み合わせることができるため、特に便利です。このようなパターンはテッセレーションと呼ばれます。

ハニカム

シナロアンミルクスネークスキン

葉の細胞構造

北アイルランドのジャイアンツコーズウェイの玄武岩柱

パイナップルの皮

亀の甲羅

人間は、古代ローマから現在まで、芸術、建築、技術におけるこれらの自然なパターンの多くをコピーしました。以下にいくつかの例を示します。

舗装パターン

イギリスのエデンプロジェクトの温室

アルハンブラのモザイク

ロンドンの大英博物館の屋根

シドニーのセルラーテセレーションパビリオン

爬虫類による平面の規則的な分割の研究 、MCエッシャー

ここでは、通常のポリゴンを使用して独自のテッセレーションを作成できます。サイドバーからキャンバスに新しいシェイプをドラッグするだけです。テッセレーションが適切な形状はどれですか？テッセレーションしない形状はありますか？面白いパターンを作ってみてください！

Examples of other students’ tessellations

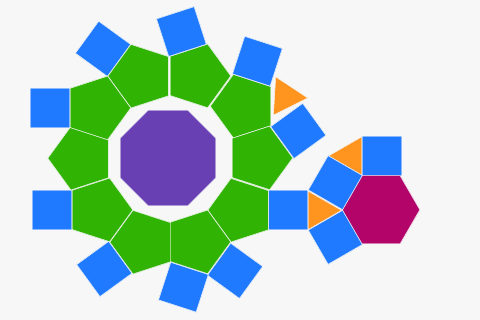
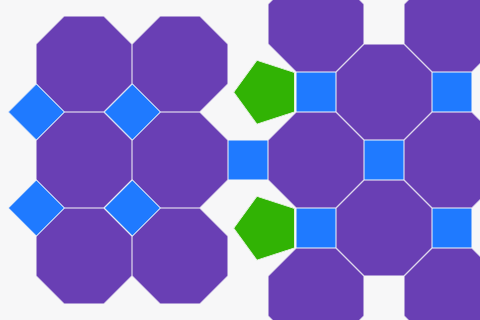
通常のポリゴンからのテッセレーション

いくつかの通常のポリゴン（ような））は非常に簡単にテッセレーションしますが、他のもの（）テッセレーションはまったくないようです。

これは、前に計算することを学んだ内角のサイズに関係しています。テッセレーションのすべての頂点で、複数の異なるポリゴンの内角が交わります。これらの角度すべてを合計して°にする必要があります。そうしないと、ギャップまたはオーバーラップが発生します。

三角形 6×60°= 360°だからです。

正方形 4×90°= 360°だからです。

ペンタゴン 108°の倍数では360°にならないからです。

六角形 3×120°= 360°だからです。

同様に、五角形のように、7辺以上の正多角形がテッセレーションされないことを確認できます。つまり、テッセレーションする通常のポリゴンは、三角形、正方形、六角形のみです。

もちろん、さまざまな種類の通常のポリゴンをテッセレーションに組み合わせることができます。ただし、それらの内角が最大360度になる場合は、次のようになります。

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°

不規則なポリゴンからのテッセレーション

不規則なポリゴンからテッセレーションを作成することもできます。ポリゴンの回転と配置に注意する必要があります。

正三角形だけでなく、 _任意の三角形を_テッセレーションできることがわかります！この図の頂点を移動してみてください。

三角形の内角の合計は°です。各角度を使用するとテッセレーションのすべての頂点で、360°を取得します。

さらに驚くべきことに_、四辺形_もテッセレーションされます！それらの内角の合計は°なので、各角度を使用するとテッセレーションのすべての頂点で、360度取得します。

ペンタゴンは少しトリッキーです。 _通常の_五角形ことはすでに見ました、通常でないものはどうですか？

五角形のテセレーションの3つの異なる例を次に示します。それらは_規則的_ではありませんが、完全に有効な5辺のポリゴンです。

これまでのところ、数学者が見つけたのは（凸）五角形の15種類のテッセレーションだけです。その最新のものは2015年に発見されました。他に何かあるのか、またはこれらの15だけが存在するのかは誰にもわかりません…

アートのテッセレーション

テッセレーションは、多くのアーティスト、建築家、デザイナー、最も有名なオランダのアーティストMCエッシャーのためのツールとインスピレーションの両方です。エッシャーの作品には、奇妙で変化する生き物、パターン、風景が含まれています。

“Sky and Water I” (1938)

“Lizard” (1942)

“Lizard, Fish, Bat” (1952)

“Butterfly” (1948)

“Two Fish” (1942)

“Shells and Starfish” (1941)

これらのアートワークは、多くの場合面白くて楽なように見えますが、基本的な数学的原理は以前と同じです：角度、回転、平行移動、ポリゴン。数学が正しくなければ、テッセレーションは機能しません！

“Metamorphosis II” by M. C. Escher (1940)

ペンローズタイル

これまでに見たすべてのテッセレーションには、1つの共通点があります。それは__周期的__です。つまり、繰り返し繰り返される規則的なパターンで構成されています。彼らはすべての方向に永遠に続くことができ、どこでも同じように見えます。

1970年代には、英国の数学者や物理学者ロジャー・ペンローズは、 _非周期的な_テッセレーションを発見した-彼らはまだ、すべての方向に無限に続けますが、まったく同じに見える_こと_はありません。これらは__ペンローズタイル__と呼ばれ、作成するのに必要なポリゴンの種類は数種類のみです。

Move the slider to reveal the underlying structure of this tessellation. Notice how you have the same patterns at various scales: the small yellow pentagons, blue stars, orange rhombi and green ‘ships’ appear in their original size, in a slightly larger size and an even larger size. This self-similarity can be used to prove that this Penrose tiling is non-periodic.

ペンローズは面白さを純粋に楽しみのために探っていましたが、実際の材料（アルミニウムなど）の内部構造も同様のパターンに従っていることがわかりました。このパターンはトイレットペーパーにも使用されました。これは、非周期的なパターンを膨らませることなく丸めることができることにメーカーが気付いたためです。

言語を変えてください

マシゴンにサインインする

シェア

進行状況をリセット