Untitled Course対称グループと壁紙
一部の形状には複数の対称性があります。簡単な例として








上記で、正方形には
また、
そして最後に、「何もしない」を別の特別な種類の対称性と考えることができます。結果は(明らかに)以前と同じだからです。これは、 __アイデンティティ__と呼ばれることもあります。
合計で、
これで、これらの対称性を使って実際にいくつかの演算を開始できます。たとえば、2つの対称を_追加_して新しい対称を取得できます。






正方形の対称性を2つ追加すると、新しい対称性が得られます。これは、自分で試すことができる「対称計算機」です。
対称計算機をいじって、パターンを見つけてみてください。これらの観察を完了することができますか?
*常に
あなたはすでにそれを追加していることに気付いたかもしれません__{.orange}対称性__は実際には追加に非常に似ています__{.green}整数__ :
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
数学では、これらのプロパティを持つすべてのコレクションは
この例では、正方形の8つの対称性から始めました。実際、すべての幾何学的形状には独自の__対称グループがあり__ます。それらはすべて異なる要素を持っていますが、常に上記の3つのルールを満たしています。
グループは数学のいたるところに現れます。要素は、数値または対称性ですが、多項式、順列、行列、関数など、3つのルールに従う_ものも使用_できます。 _群論_の鍵となる考え方は、個々の要素には興味がないということです。 _それらが互いにどのように相互作用するかという点_にのみ興味があります。
たとえば、異なる分子の対称グループは、科学者が対応する材料の特性を予測および説明するのに役立ちます。
グループは、ボードゲームでの勝利戦略、医学におけるウイルスの挙動、音楽におけるさまざまな調和、および他の多くの概念の分析にも使用できます…
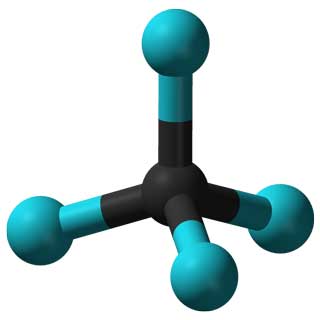
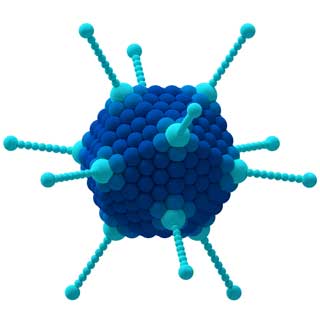
CCl 4分子(左)とアデノウイルス(右)の特性は、それらの対称性によって決まります。
壁紙グループ
前のセクションでは、回転と反射という2つの異なる変換に対応する2種類の対称性について説明しました。しかし、また、剛体変換の三種類の対称性があります:


六角形のホーニッコム


セラミック壁タイル
反射、回転、並進の対称性に加えて、第4の種類、


パターンは、複数のタイプの対称性を持つことができます。そして、正方形の場合と同様に、パターンの
これらのグループは、パターン_が_どのように表示されるか(色や形など)についてはあまり説明せず、 _繰り返される_方法についてのみ説明します。同じように配置され、繰り返される限り、複数の異なるパターンが同じ対称性グループを持つことができます。


これらの2つのパターンは非常に異なって見えますが、同じ対称性を持っています。しかし、対称性は色や表面的な形ではありません。


これらの2つのパターンは、対称性が同じです。ただし、左側の対応するパターンに似ていますが、互いに似ています。
可能なパターンは無限にありますが、それらはすべて17の異なる対称グループの1つを持っていることがわかります。これらは__壁紙グループ__と呼ばれ__ます__ 。すべての壁紙グループは、平行移動、回転、反射、グライド反射の組み合わせによって定義されます。これらの例

Group 1 – P1
Only translations div img(src="/content/transformations/images/wallpapers/p2.svg" width=360, height=240) p.caption Group 2 – P2 Rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p3.svg" width=360, height=240) p.caption Group 3 – P3 Rotations of order 3 (120°), translations div img(src="/content/transformations/images/wallpapers/p4.svg" width=360, height=240) p.caption Group 4 – P4 Four rotations of order 2 (180°), translations div img(src="/content/transformations/images/wallpapers/p6.svg" width=360, height=240) p.caption Group 5 – P6 Rotations of order 2, 3 and 6 (60°), translations div img(src="/content/transformations/images/wallpapers/pm.svg" width=360, height=240) p.caption Group 6 – PM Parallel axes of reflection, translations div img(src="/content/transformations/images/wallpapers/pmm.svg" width=360, height=240) p.caption Group 7 – PMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p4m.svg" width=360, height=240) p.caption Group 8 – P4M Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p6m.svg" width=360, height=240) p.caption Group 9 – P6M Rotations (ord 2 + 6), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p3m1.svg" width=360, height=240) p.caption Group 10 – P3M1 Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p31m.svg" width=360, height=240) p.caption Group 11 – P31M Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p4g.svg" width=360, height=240) p.caption Group 12 – P4G Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/cmm.svg" width=360, height=240) p.caption Group 13 – CMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pmg.svg" width=360, height=240) p.caption Group 14 – PMG Reflections, glide reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pg.svg" width=360, height=240) p.caption Group 15 – PG Parallel glide reflections, translations div img(src="/content/transformations/images/wallpapers/cm.svg" width=360, height=240) p.caption Group 16 – CM Reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/pgg.svg" width=360, height=240) p.caption Group 17 – PGG Perpendicular glide reflections, rotations of order 2, translations
残念ながら、これらのグループが_17個_ある単純な理由はなく、それを証明するにはより高度な数学が必要です。代わりに、17の壁紙グループのそれぞれに独自の繰り返しパターンを描画してみることができます。
Examples of other students’ drawings



壁紙グループはすべて、フラットな2次元パターンについてのものでした。 3次元パターンについても同様のことができます。これらは結晶学的グループと呼ばれ、219あります。
平行移動、反射、回転、グライド反射に加えて、これらのグループには__グライド平面__や__ねじ軸__などの対称性が含まれます(ボトルのねじを外すときの動きについて考えてください)。
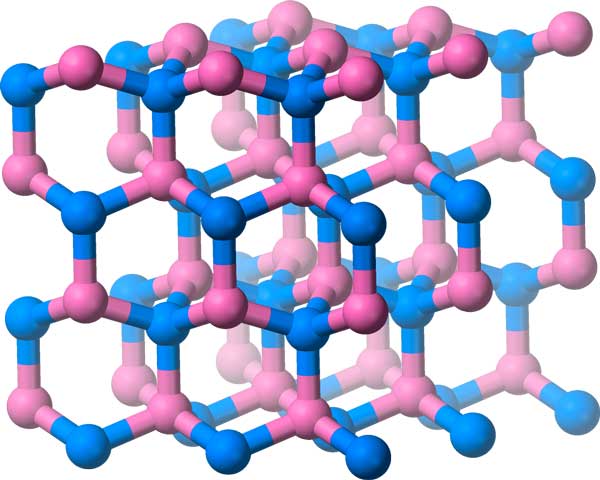
窒化ホウ素は、分子がこの結晶格子に配置されており、3次元の対称グループを持っています。