フラクタルマンデルブロセット
前の章で見たフラクタルはすべて、反復 のプロセスを使用して作成されました。特定のパターンから始めて、それを何度も繰り返します。




これは、前に見た数学の別の概念に似ています。
例として再帰的な式
開始値
これまでのところ、新しいことは何も学んでいません。ただし、約1世紀前に、数学者は、実際の数直線だけでなく、
ジュリアセット
以前と同じシーケンス
ご覧のように、
では、もう少し難しくしましょう。以前の数値を単に2乗するのではなく、定数_{.pill.red} c_を毎回追加します(これは任意の複素数にすることができます)。つまり、
この図では、
場合によっては、シーケンスが_1つのポイント_に収束せず、三角形のように複数のポイントのサイクルに達することがあります。これらのサイクルは、軌道 と呼ばれます。
青色で表示されている点は、対応するシーケンスが収束しているか、軌道を持っていることを意味します(境界 であると言います)。白のままになっている点は、対応するシーケンス 発散 を意味します。境界がなく、最終的には無限に膨らみます。
数字で色分けして形成されるさまざまな形状は、
当時、ジュリアのセットが実際にどのように見えるかを視覚化するのに役立つコンピューターはありませんでした。ジュリアやファトウのような数学者は数学的にそれらについて推論することができましたが、彼らは今まで自分たちがどのように見えるかもしれないラフな手描きのスケッチを見ただけでした。
今日、この問題は発生していません。下の画像はすべて異なるジュリアセットです。異なる色は、その時点でのシーケンスが発散する_速さ_を示します。
マンデルブロセット
さまざまなジュリアセットを作成するときに、すべてのシーケンスが発散する_c_の値がいくつかあり、複雑な平面全体が白のままであることに気付いたかもしれません。ジュリアとファトウの数十年後、新世代の数学者がこれらの領域がどのように見えるかをマッピングしようとしました。
前の例では、
もう一度、複雑な平面の上にペイントして、シーケンスが制限されたままの領域を明らかにします。どんな形が出ると思いますか?

このフラクタルは
数年後、
すべてのフラクタルと同様に、マンデルブロ集合を永久に「拡大」して、あらゆるスケールで新しいパターンを見つけることができます。ここでは、タツノオトシゴの谷 と呼ばれるマンデルブロセットの一部を拡大できます。黒点は、シーケンスが制限されているマンデルブロ集合の_内部_です。色付きの点は、シーケンスが分岐するマンデルブロ集合の_外側_であり、異なる色は、無限に成長する_速さ_を示します。

















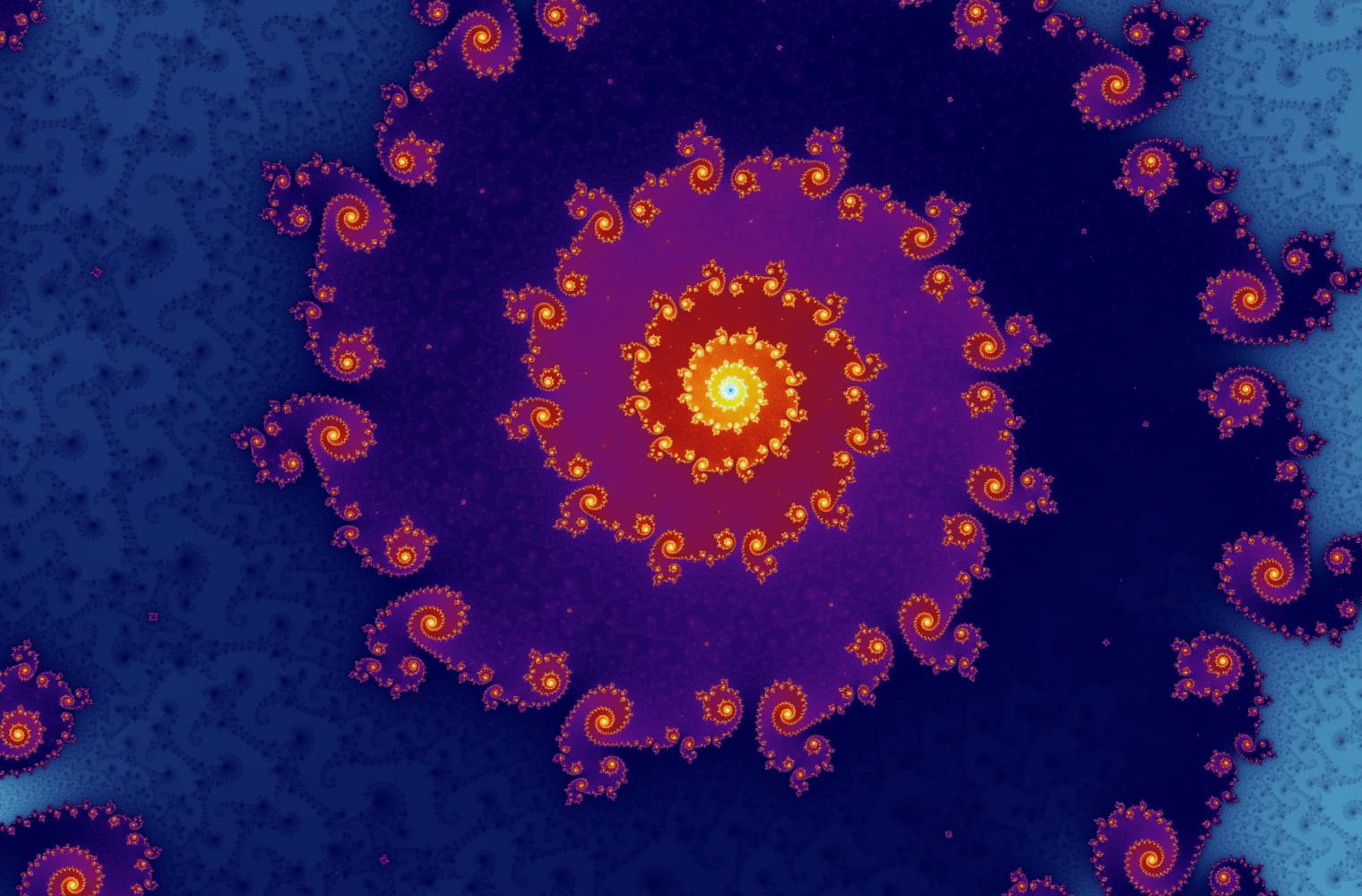

このスライダーは27の個別の画像で構成され、最大14兆を超えるズームレベル、つまり

マンデルブロ集合内で cの値を移動すると、奇妙なプロパティに気付くでしょう:
- マンデルブロ集合の本体内のすべてのシーケンスは、を単一点に収束させます。
- 上部の大きな電球 内のシーケンスは、
ポイントで構成される軌道 に到達します。 - この小さい電球 のシーケンスは、軌道の長さが
です。
すべての球根には異なるサイズの軌道があり、小さい球根は軌道のポイントがますます増えています。これらの軌道のサイズは、カオス理論 の重要な概念である ロジスティックマップ と密接に関連しています。
ベルノアットマンデルブロは、彼の人生のほとんどをフラクタルの研究と、_ラフネス_と_自己相似性_の数学に捧げました。彼の作品は、物理学、気象学、神経学、経済学、地質学、工学、コンピューターサイエンス、および他の多くの分野で応用されていました。
1985年、マンデルブロセットは_Scientific American_誌の表紙に登場し、それ以来、世界で最も有名な数学的形状の1つになりました。 Tシャツやミュージックビデオ、スクリーンセーバーとして見つけることができ、多くの人気のある本や映画で使用されています。