English
عربى
中文
Deutsch
Español
Français
हिन्दी
Hrvatski
Italiano
日本語
Português
Română
Русский
Svenska
Türkçe
Tiếng Việtフラクタルはじめに
自然を見回すと、次のような複雑な植物に気づいたかもしれません。
この シダ は、大きな葉から枝分かれした多くの小さな葉で構成されています。
この__ロマネスコブロッコリー__は、より大きな
最初は、これらは非常に複雑な形状のように見えますが、よく見ると、どちらも比較的単純なパターンに従っていることに気付くでしょう：植物のすべての個々の部分は、全体とまったく同じに見えます植物、ちょうど小さい。同じパターンが小さなスケールで何度も繰り返されます。
数学では、このプロパティを 自己相似性 と呼び、それを持つ形状を
独自のフラクタルを作成するには、単純なパターンから始めて、小さなスケールで繰り返します。
最も単純なパターンの1つは、ラインセグメントで、もう2つのセグメントが一方の端から分岐しています。このパターンを繰り返すと、これらの青いセグメントの両方に、その端にさらに2つの分岐があります。
青い点を移動して、すべての枝の長さと角度を変更できます。次に、下の
枝の位置に応じて、上の、、またはのように、完全に異なるパターンを作成できます。他に何が見つかりますか？
もう1つの有名なフラクタルは、
最終形状がそれ自体の3つの同一のコピーで構成され、これらのそれぞれが三角形全体のさらに小さなコピーで構成されていることに注意してください！あなたは永遠に三角形をズームインし続けることができ、パターンと形は常に繰り返され続けます。
この章の冒頭にある植物は、フラクタルのように_見えます_が、実際に_真の_フラクタルを作成することは明らかに不可能です。同じパターンを何度も何度も繰り返し続けると、最終的には分割できない細胞、分子、または原子に到達することになります。
ただし、数学を使用すると、実際のフラクタルが「持つ」はずの性質について考えることができます。これらは非常に驚くべきことです...
フラクタル次元
まず、フラクタルの次元について考えてみましょう。線の寸法は
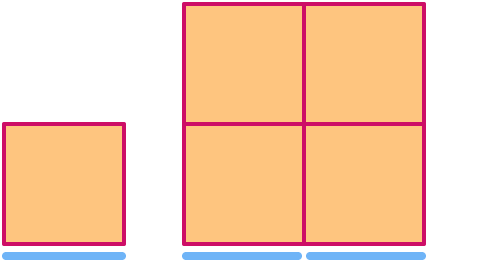
正方形の寸法は
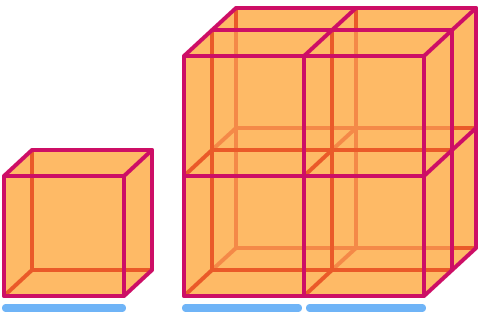
キューブのディメンションは
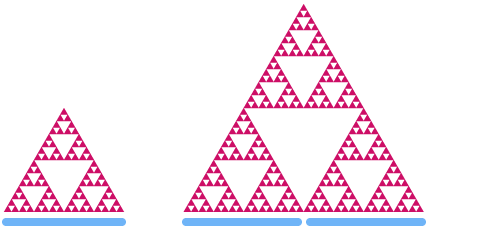
次に、シェルピンスキーの三角形を見てみましょう。 2倍に拡大すると、「面積」が
_d_がシェルピンスキー三角形の次元であるとしましょう。上記と同じパターンを使用して、
しかし、ちょっと待って…何かが整数ではない次元を持つことができるのでしょうか？それは不可能に思えますが、これはフラクタルの奇妙な特性の1つにすぎません。実際、これがフラクタルに彼らの名前を与えるものです：彼らは 分数次元 を持っています。
すべての反復で、シェルピンスキー三角形の一部の領域を削除します。これを無限に実行できるとしたら、実際には領域が残っていないことになります。そのため、シェルピンスキーの三角形は2次元の領域と1次元の線の間にあるものです。
多くのフラクタルは 自己相似 ですが、より適切な定義は、フラクタル が 非整数次元 を持つ形状であるということです。
コッホスノーフレーク
自然にはフラクタルのような形がたくさんあります。この章の初めにすでにいくつかの植物を見てきました。他の素晴らしい例は雪片と氷の結晶です：
独自のフラクタルスノーフレークを作成するには、繰り返し適用できる簡単な手順をもう一度見つける必要があります。
シェルピンスキーの三角形と同様に、単一の正三角形から始めましょう。ただし、すべてのステップで小さな三角形を_削除_するのではなく、エッジに沿って小さな三角形を_追加_します。すべての三角形の辺の長さは、前のステップの三角形の
結果の形状は
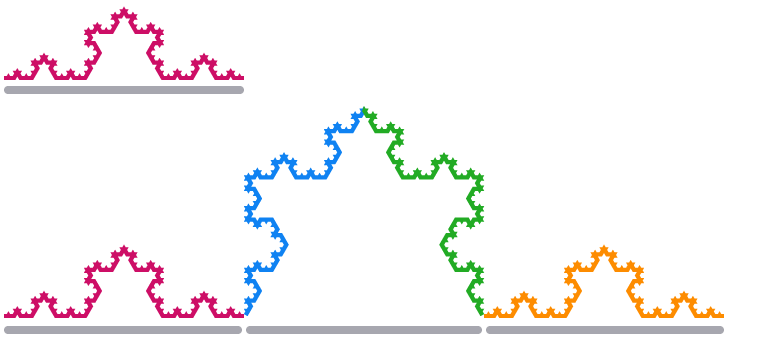
コッホスノーフレークの1つのエッジセグメントを3倍に拡大すると、その長さは
上記と同じ次元とスケール係数の関係を使用して、式
エリア_{span.check(when="blank-6")}_
Kochスノーフレークの作成は、
最初の反復の後、追加される新しい三角形の数は、すべてのステップで
無限の
境界
Kochスノーフレークの周長を計算することもできます。すでに見てきたように、周囲の長さはステップごとに
これは、もう一度、幾何学的な系列があることを意味します。ただし、この場合、
これが直観に反するように見える場合は、すべてのステップで境界に
_有限_の領域と_無限_の円周を持つ形状を作成できるとは考えられませんが、これはフラクタルの予期しない多くの特性の1つにすぎません。
独自のフラクタルを作成する他の方法を考え出すことはできますか？
「凍ったフラクタルに私の魂は渦巻いている…」
メンガースポンジ
上記の例のように、フラクタルは「フラット」である必要はありません。 3次元に見える最も有名なフラクタルの1つは、1926年に初めてそれを説明した数学者
私たちは固体の立方体から始め、その側面に次第に小さな穴をあけます。穴の新しい繰り返しごとに、前の穴の繰り返しの幅が
これで、上記のKochスノーフレークの場合と同じように、メンガースポンジの寸法_d_を計算することができます。この場合、
無限に何度も穴を空けることを想像すると、実際のボリュームは残っていません。そのため、立方体は「完全ではない」3次元です。
フラクタル海岸線
これまでに見たすべてのフラクタルの主要な特徴の1つは、いつまでも「ズームイン」して、常に新しいパターンを見つけることができることです。 1920年頃、イギリスの数学者
国の基本的な形状から始めて、ズームインすると、河川の入り江、入り江、河口を追加し、次に個々の崖、岩、小石などを追加します。
これは、国の境界線の長さを計算しようとするときに重大な問題です。どのくらいズームインするか、どの隅と隅を含めるかをどのように決定しますか？
たとえば、イギリスの海岸線の長さを測定する方法の1つは、長い定規を使って、ビーチを一周して、すべての距離を合計することです。
ルーラーが
どんどん小さくしていく定規を使い続けるだけで、海岸線の長さの結果が少しずつ長くなります。以前のコッホスノーフレークと同じように、イギリスの海岸線は無限に長いようです。これはしばしば 海岸線パラドックス と呼ばれます。
数十年後、数学者
英国の海岸線は確かにフラクタルを「見ている」が、これまでに見た他のフラクタルとは異なり、_自己相似_ではない。そのサイズを見つけるために、グリッド上にそれを描画し、それが交差するセルの数を数えることができます。
最初は、 88 個の交差するセルがあります。海岸線を2倍に拡大すると、交差するセルは 197 であり、2倍以上になります。
海岸線のサイズは
これをより大きなグリッドで繰り返すと、英国の海岸線の寸法は実際には約1.21であることがわかります。マンデルブロは、このフラクタル次元が形状の ラフネス の尺度でもあることに気づきました。彼は、数学と科学の他の多くの分野で重要なアプリケーションを見つけた新しい概念です。
自然と技術におけるより多くのフラクタル
本当のフラクタルは自然界には決して現れませんが、フラクタルのように_ほとんど_見えるオブジェクトがたくさんあります。すでに植物、雪片、海岸線を見てきましたが、さらにいくつかの例を次に示します。
中央アジアの山脈
インドのガンジス川デルタ
稲妻
網膜の血管
アメリカのグランドキャニオン
雲
これらのオブジェクトはすべて完全にランダムに見える場合がありますが、フラクタルと同様に、オブジェクトの形成方法を決定する基本的なパターンがあります。数学は形状をよりよく理解するのに役立ち、フラクタルは医学、生物学、地質学、気象学などの分野での用途があります。
コンピュータ生成のフラクタル地形
また、フラクタルを使用して、自然のリアルな「コピー」を作成することもできます。たとえば、ビデオゲームやコンピューター生成の映画で使用される風景やテクスチャなどです。この画像の水、山、雲はすべてフラクタルの助けを借りてコンピューターで作成されています！
また、このプロセスを逆にしてデジタル画像を圧縮し、ファイルサイズを小さくすることもできます。最初のアルゴリズムは1980年代にマイケルバーンズリーとアランスローンによって開発され、現在も新しいアルゴリズムが研究されています。